Здравствуйте, уважаемые читатели блога Goldbusinessnet.com. В ходе развития современных компьютерных и интернет-технологий наиважнейшее значение приобретают единицы измерения, необходимые при хранении и передаче информации, коими являются бит и байт.
Все данные хранятся или передаются в закодированном цифровом формате, потому возможность измерить их объем позволяет обеспечить системность и устойчивость в работе с ними.
По аналогии с известными физическими единицами измерения, которые при большой их величине для удобства исчисления получают увеличительные приставки (1000 метров = 1 километр, 1000 грамм = 1 килограмм), байт тоже имеет свои производные (килобайт, мегабайт, гигабайт и т.д.).

Однако, в случае бита и байта существуют свои особенности, связанные с цифровой сущностью системы, которые ниже будут подробно разъяснены. Кроме того, будут рассмотрены соотношение между байтом и битом, суть понятия «машинное слово» и другие нюансы.
Единицы измерения информации бит (bit) и байт (byte)
Чтобы стало понятнее, придется изложить все поподробнее и начать, так сказать, с истоков. Однако, постараюсь донести информацию без заумных математических формул и терминов. Начнем с того, что существует несколько позиционных систем счисления. Все их перечислять нет необходимости, но для ясности остановимся на двух основных.
Десятичная и двоичная системы счисления
Самая известная из них, с которой мы все сталкиваемся ежедневно, это десятичная система. В ней любое число состоит из цифр (от 0 до 9), каждая из которых принадлежит определенному разряду. Разрядность увеличивается справа налево (единицы, десятки, сотни, тысячи и т.д.).
Возьмем для примера число 249, которое можно представить в виде суммы произведений цифр на 10 в степени, соответствующей данному разряду:
249 = 2×102 + 4×101 + 9×100 = 200 + 40 + 9
Таким образом, нулевой разряд — это единицы (100), первый — десятки (101), второй — сотни (102) и так далее. В компьютере, как и в других электронных устройствах, вся информация распределяется по файлам (здесь о файловой системе подробности) и кодируется соответствующим образом в цифровом формате, причем в силу простоты использования применяется двоичная система счисления, на которой остановлюсь отдельно.
В двоичной системе числа представляются посредством всего двух цифр: 0 и 1. Попробуем записать уже рассмотренное нами число 249 в двоичной системе, чтобы понять ее суть. Для этого делим его на 2, получив целое частное с остатком 1. Эта единичка и будет самым младшим разрядом, который будет, как и в случае десятичной системы, крайним справа.
Далее продолжаем операцию деления и каждый раз целые числа также делим на 2, получая при этом в остатке 0 или 1. Их последовательно и записываем справа налево, получив в итоге 249 в двоичной системе. Деленин следует проводить до тех пор, пока в итоге не появится нуль:
249/2 = 124 (остаток 1) 124/2 = 62 (остаток 0) 62/2 = 31 (остаток 0) 31/2 = 15 (остаток 1) 15/2 = 7 (остаток 1) 7/2 = 3 (остаток 1) 3/2 = 1 (остаток 1) 1/2 = 0 (остаток 1)
Теперь записываем нули и единички в остатке последовательно справа налево и получаем наше подопытное число в двоичной системе:
11111001
Чтобы не осталось темных пятен, проведем обратное действие и попробуем перевести то же самое число из двоичной в десятичную систему, проверив заодно правильность выше изложенных действий. Для этого умножаем опять же по порядку слева направо нуль или единицу на 2 в степени, соответствующей разряду (по аналогии с десятичной системой):
1×27 + 1×26 + 1×25 + 1×24 + 1×23 + 0×22 + 0×21 + 1×20 = 128 + 64 + 32 + 16 + 8 + 0 + 0 + 1 = 249
Как видите все получилось, и мы смогли преобразовать число, записанное в двоичной системе, на его запись в десятичной системе счисления.
Соотношение битов и байтов в информатике
Я не зря предоставил чуть выше краткий математический экскурс, поскольку именно двоичная система служит основой измерения, используемой в электронных устройствах. Базовой единицей количества информации, равной разряду в двоичной системе, как раз и является бит.
Этот термин происходит от английского словосочетания binary digit (bit), что означает двоичное число. Таким образом, бит может принимать лишь только два возможных значения: 0 или 1. В информатике это означает два совершенно равных с точки зрения вероятности результата («да» или «нет») и при этом не допускается никакого другого толкования.
Это очень важно с точки зрения корректной работы системы. Двигаемся дальше. Количество бит, которое обрабатывается компьютером в один момент, называется байтом (byte). 1 байт равен 8 битам и, соответственно, может принимать одно из 28 (256) значений, то есть от 0 до 255:
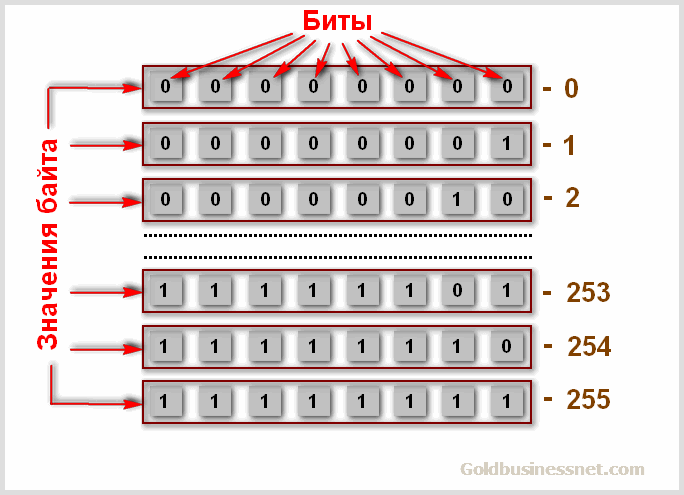
Итак, нам теперь доподлинно известно, что такое байт, и какую роль он играет в качестве единицы измерения при работе с информацией, хранящейся и обрабатываемой в цифровом виде. Кстати, в международном формате байт может обозначаться двумя способами — byte или B.
Перевести числа в десятичном формате на двоичную систему можно при помощи калькулятора. Если у вас ОС Windows 7, то вызвать этот инструмент можно так: «Пуск» — «Все программы» — «Стандартные» — «Калькулятор». В десятке это можно сделать из списка приложений либо просто введя в поисковую строку слово «Калькулятор»):
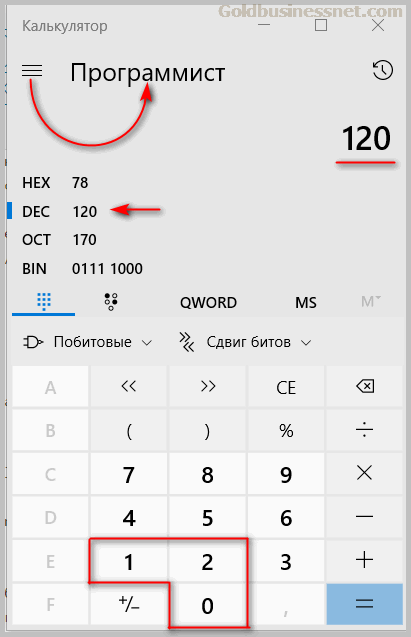
В меню «Вид» выбираете формат «Программист» и вводите желаемое число (например, 120):
Напротив опции «BIN» мы видим запись данного числа в двоичной системе:
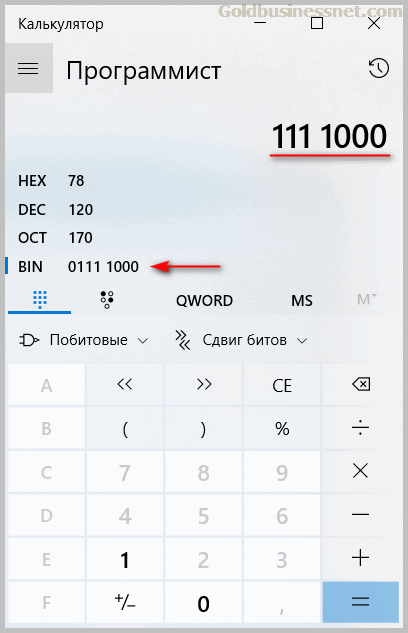
На что здесь следует обратить внимание? Во-первых, в строке справа вверху представлены лишь семь разрядов (биты со значениями ноль или единица):
111 1000
Здесь все просто. Если самый старший разряд (бит), расположенный крайним слева, принимает значение 0, то он просто не записывается. Два или более нулевых бита тоже опускаются (по аналогии с десятичными числами — ведь к сотням мы не прописываем 0 тысяч, например).
Доказательством может служить полная запись полученного числа напротив «BIN»:
0111 1000
Если вы внимательны, то увидите, что здесь во-вторых. Это способ записи в виде двух частей, каждая из которых состоит из четырех бит. В информатике используется еще такое понятие как полубайт, или ниббл (nibble). Это удобно тем, что ниббл можно представить как разряд в шестнадцатеричной системе, которая широко используется в программировании.
Понятие машинного слова
Выше мы поговорили о том, что байт содержит восемь бит. Это позволяет выразить 256 (два в восьмой степени) разных значений. Однако на практике в основном этого далеко не достаточно и во многих случаях приходится использовать не один, а несколько byte. В качестве примера воспользуемся еще раз калькулятором Windows и переведем число 1000 в двоичную систему:
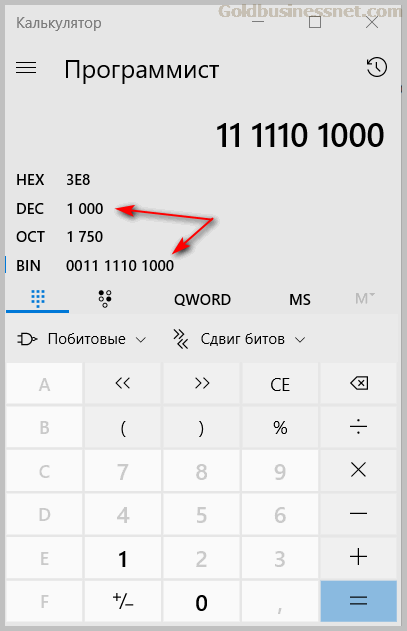
Как видите, для этого пришлось отщипнуть пару разрядов из второго байта. На практике для обработки достаточно объемной информации в компьютерах применяется такое понятие как машинное слово, которое может содержать 16, 32, 64 bit.
С их помощью можно выразить соответственно 216, 232 и 264 различных значений. Но в этом случае нельзя говорить о 2, 4 или 8 байтах, это немного разные вещи. Отсюда растут ноги из упоминания, например, 32-, 64-разрядных (-битных) процессоров или других устройств.
Сколько байт в килобайте, мегабайте, гигабайте, терабайте
А теперь самое время перейти к производным байта и представить, какие приставки увеличения здесь используются. Ведь байт как единица очень маленькая величина, и для удобства очень даже полезно использовать аналоги, которые бы обозначали 1000 B, 1 000 000 B и т.д. Здесь тоже есть свои нюансы, о которых и поговорим ниже.
Строго говоря, для представления величин корректно использовать приставки для двоичной системы счисления, которые кратны 210 (1024). Это кибибайт, мебибайт, гебибайт и т.д.
1 кибибайт = 210 (1024) байт 1 мебибайт = 210 (1024) кибибайт = 220 (1 048 576) байт 1 гебибайт = 210 (1024) мебибайт = 220 (1 048 576) кибибайт = 230 (1 073 741 824) байт 1 тебибайт = 210 (1024) гебибайт = 220 (1 048 576) мебибайт = 230 (1 073 741 824) кибибайт = 240 (1 099 511 627 776) байт
Но данные словосочетания не прижились в широком использовании. Возможно, одной из причин стала их неблагозвучность. Поэтому пользователи (и не только) повсеместно употребляют вместо двоичных десятеричные приставки (килобайты, мегабайты, гигабайты, терабайты), что является не совсем корректным, поскольку по сути (в соответствии с правилами десятичной системы счисления) это означает следующее:
1 килобайт = 103 (1000) байт 1 мегабайт = 103 (1000) килобайт = 106 (1 000 000) байт 1 гигабайт = 103 (1000) мегабайт = 106 (1 000 000) килобайт = 109 (1 000 000 000) байт 1 терабайт = 103 (1000) гигабайт = 106 (1 000 000) мегабайт = 109 (1 000 000 000) килобайт = 1012 (1 000 000 000 000) байт
Но раз уж так сложилось, ничего не поделаешь. Важно лишь помнить, что на практике часто используются килобайт (Кбайт), мегабайт (Мбайт), гигабайт (Гбайт), терабайт (Тбайт) именно в качестве производных от байта как единицы измерения информации в двоичной системе. И в этом случае употребляют, например, термин «килобайт», имея ввиду именно 1024 байт.
Однако, очень часто производители накопителей (включая жесткие диски, флэшки, DVD- и CD-диски) при указании объема для хранения информации применяют именно десятичные приставки по прямому назначению (1 Кбайт = 1000 байт), в то время как тот же Виндовс, например, рассчитывает их размер в двоичной системе.
Отсюда и выходит некоторое несоответствие, которое может запутать простого пользователя. Скажем, в документации указана емкость диска 500 Гб, в то время как Windows показывает его объем равным 466,65 Гбайт.
По сути никакого расхождения нет, просто размер накопителя присутствует в разных системах счисления (тот же пень, только сбоку). Для неопытных юзеров это крайне неудобно, но, как я уже сказал, приходится с этим мириться.
Резюмируя, отмечу следующее. Скажем, вам зададут вопрос: сколько байт в килобайте? Теоретически корректным будет ответ: 1 килобайт равен 1000 байтам. Просто надо помнить, что на практике по большей части десятичные приставки используются в качестве двоичных, которые кратны 1024, хотя иногда они применяются по прямому назначению и кратны именно 1000.
Вот такая арифметика, надеюсь, что вы не запутались. В публикации я упомянул килобайт, мегабайт, гигабайт и терабайт, а что дальше? Какие еще более крупные единицы количества информации возможны? На этот вопрос ответит таблица, где указаны не только соотношение единиц в обеих системах, но и их обозначения в международном и российском форматах:
| Двоичная система | Десятичная система | ||||||
|---|---|---|---|---|---|---|---|
| Название | Обозначение | Степень | Название | Обозначение | Степень | ||
| Рос. | Межд. | Рос. | Межд. | ||||
| байт | Б | B | 20 | байт | Б | B | 100 |
| кибибайт | КиБ | KiB | 210 | килобайт | Кбайт | KB | 103 |
| мебибайт | МиБ | MiB | 220 | мегабайт | Мбайт | MB | 106 |
| гибибайт | ГиБ | GiB | 230 | гигабайт | Гбайт | GB | 109 |
| тебибайт | ТиБ | TiB | 240 | терабайт | Тбайт | TB | 1012 |
| пебибайт | ПиБ | PiB | 250 | петабайт | Пбайт | PB | 1015 |
| эксбибайт | ЭиБ | EiB | 260 | эксабайт | Эбайт | EB | 1018 |
| зебибайт | ЗиБ | ZiB | 270 | зеттабайт | Збайт | ZB | 1021 |
| йобибайт | ЙиБ | YiB | 280 | йоттабайт | Ибайт | YB | 1024 |
Ежели желаете быстро определить, например, сколько мегабайт в гигабайте (хотя опытный юзер легко обойдется в этом случае без таблицы), то ищите в таблице ячейки, соответствующее числу байт в мегабайте и гигабайте, а затем делите большее значение на меньшее.
109/106 = 1 000 000 000/1 000 000 = 1000
Получается, что в 1 гигабайте 1000 мегабайт. Точно также можно переводить производные в двоичной системе — мебибайты в кибибайты, тебибайты в гибибайты и т.д.
Используем конвертер для перевода битов и байтов
Публикация была бы неполной, если бы я не привел инструмент, с помощью которого можно осуществить перевод byte в различные производные. В сети много разнообразных конвертеров, посредством которых можно произвести эти операции. Вот один из них, который мне приглянулся.
Этот конвертер удобен тем, что введя количество byte, можно сразу получить результат во всех возможных измерениях (в том числе перевести биты в байты):

Из данного примера следует, что 3072 байта равно 24576 битам, 3,0720 килобайтам или 3 кибибайтам. Кроме этого, чуть ниже расположены ссылки на миникалькуляторы, где вы сможете быстро произвести конкретный перевод из одной системы единиц в другую.









Здравствуйте. Отличный материал! Огромная Вам благодарность! Всё понятно и доступно, но из-за путаницы пока не запомнил, буду повторять.
Очень интересна информация о составе байта, как расшифровать правильно эти самые 8 бит. Можно по подробнее о значениях 1 и 0 в бите? На примере с числом 249 всё понял. А что с буквами?
Здравствуйте!
Интересная статья! Но я бы добавил о практическом применении понятий бит и байт. Бит, в основном, используется для определения скорости передачи данных в сетях, а байт для получения объёма той или иной информации. Хотя, например, тот же Windows использует байт как скорость передачи данных.
Alex, спасибо, полезное уточнение.
Всегда интересовало где, чего и сколько. Спасибо за статью!!!
Пожалуйста, Антон.
Спасибо за статью. Было очень интересно узнать, что идёт дальше после терабайта.
Пожалуйста, Александр. Хотя практически значение таких величин в жизни простого пользователя стремится к нулю.